11.10 - Bump / Normal Maps¶

The previous chapter explained how to model light. Both the diffuse and specular lighting calculations require a normal vector. In lesson 11.3 we discussed two scenarios for defining the normal vectors:

Flat Shading - one normal vector for a triangle. The diffuse color for a triangle is identical for all of its fragments.
Smooth Shading - each vertex has a separate normal vector. This vector is typically an average of the normal vectors from the adjacent triangles. Interpolating the vertex normal vectors across the surface produces a distinct normal vector for each fragment. However, the normal vectors change uniformly across the surface which causes the color to change uniformly across the surface.

Let’s investigate a third option: a distinct normal vector for every fragment of a triangle. Texture mapping allows the retrieval of a unique color for each fragment. Could texture mapping techniques be used to retrieve a unique normal vector for each fragment? YES! And there are two standard techniques:

A bump map uses information from a texture map to modify a flat or smooth shaded normal vector.
A normal map uses a texture map to retrieve a distinct normal vector.

Changing the normal vector for each fragment changes the percentage of diffuse and specular light that is reflected, thus allowing for the simulation of surface variations on a triangle’s face.

Bump Maps¶

Bump maps can be image-based or procedural-based. In the case of images, the image is assumed to be a greyscale image that contains a single intensity value per pixel. In the case of procedural texture maps, a single percentage value is calculated in the range [0.0,1.0].

The details to implement bump mapping are non-trivial, so let’s start with the big idea:

Each vertex of a triangle has a normal vector. The vertex shader puts the normal vector into a varying variable and each fragment gets an interpolated normal vector.
The fragment shader uses a texture map to get a <deltaX,deltaY> offset to modify its normal vector. This “tweak” in the normal vector must be applied relative to the triangle’s orientation. Therefore, each triangle must be able to calculate or retrieve a local coordinate system. The deltaX offset must be applied in a direction that is “to the right” relative to the triangle’s surface. Similarly, the deltaY offset must be applied in a direction that is “upward” relative to the triangle’s surface.
The diffuse and specular lighting calculations are performed using the new normal vector.

There are two major tasks in step 2: produce a (deltaX,deltaY) offset from a texture map and use a triangle’s local coordinate system to modify a fragment’s normal vector.

Getting the Normal Vector Offsets¶

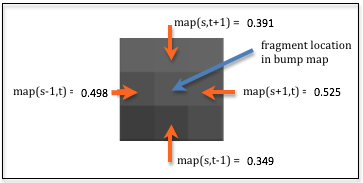
../_images/bump_map_finite_difference.png

For a texture map implemented using a “bump map image” a (deltaX,deltaY) offset can be calculated from the four surrounding pixels of the fragment’s location in the bump map image. The amount of relative change around the image location can be calculated using the difference between values in the horizontal and vertical directions. (In mathematics this is called a “finite difference.”) The diagram to the right shows nine pixels in an enlarged area of an image where the difference between the horizontal pixels is 0.027, i.e., (0.525 - 0.498), and the difference between the vertical pixels is 0.042, i.e., (0.391 - 0.349). This gives a offset to modify the surface normal vector that is proportional to the changes in the bump map image. In the diagram’s example the offset vector is <0.027, 0.042>.

In a fragment shader the normal vector offsets can be calculated using the following example code. To retrieve adjacent pixels, the amount of change in the texture coordinates can be calculated by dividing the image dimensions into 1.0. For example, if the image has a width of 512 pixels, 1.0/512.0, (i.e., 0.001953125) needs to added to a u texture coordinate to get to its adjacent pixel.

// The dimensions of the bump map image: (width, height)
uniform vec2 u_Image_size;

//-------------------------------------------------------------------------
// Given texture coordinates, calculate the "finite difference"
// between neighboring pixels.
vec2 get_bump_offsets(vec2 texture_coordinates) {
  float pixel_delta_u = 1.0 / u_Image_size[0];
  float pixel_delta_v = 1.0 / u_Image_size[1];

  vec2 up    = vec2(0.0,  pixel_delta_v);
  vec2 down  = vec2(0.0, -pixel_delta_v);
  vec2 left  = vec2(-pixel_delta_u, 0.0);
  vec2 right = vec2( pixel_delta_u, 0.0);

  vec4 right_color = texture2D(u_Texture_unit, texture_coordinates + right);
  vec4 left_color  = texture2D(u_Texture_unit, texture_coordinates + left);
  vec4 up_color    = texture2D(u_Texture_unit, texture_coordinates + up);
  vec4 down_color  = texture2D(u_Texture_unit, texture_coordinates + down);

  return vec2(right_color[0] - left_color[0], up_color[0] - down_color[0]);
}

Modifying a Normal Vector¶

Just as a model has a local coordinate system, every triangle in a model has its own local coordinate system. The normal vector of a triangle vertex points away from the triangle’s front face. Let’s assume the normal vector is equivalent to the Z axis of the triangle’s local coordinate system, and the equivalent X and Y axes lie in the plane defined by the triangle’s surface. We can solve for the vectors that represent the X and Y axes such that they have an equivalent orientation to the axes of the texture map.

In the diagram below, the left diagram shows a triangle in “texture coordinate space.” Regardless of the actual dimensions of the texture map image, the U and the V axes have unit length and the texture coordinates (u1,v1), (u2,v2), and (u3,v3) are percentages in the range [0.0,1.0]. The normal vector for the triangle is coming out of the diagram towards you. In the right diagram is a 3D plot of the same triangle. The vectors U3d and V3d can be calculated such that they lie in the plane defined by the triangle and they are consistent with the orientation of the texture map. Said another way, we want to calculate where U and V would be in 3D space if the texture map was placed on the surface of the 3D triangle.

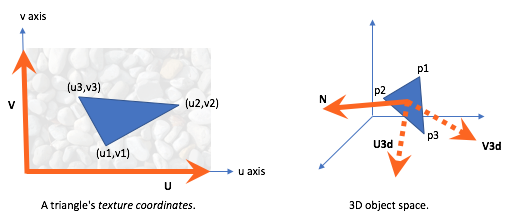
Vector Math

All vectors are defined with reference to a coordinate system. For example, <3,4> is a vector that changes 3 units along the X axis and 4 units along the Y axis. The vector can be represented as the sum of two vectors, 3*<1,0> + 4*<0,1>. The axis vectors, <1,0> and <0,1>, are the “basis” for the definition. Any vector can be represented by the sum of two scaled “basis” vectors.

In the “3D space” diagram above, the vectors <p3-p1> and p2-p1 can be represented using the vectors U3d and V3d as their “basis”. The “lengths” applied to the “basis” vectors comes from the corresponding vectors in the “texture coordinates space”. This provides the following two equations:

<p2-p1> = (u2-u1)*U3d + (v2-v1)*V3d
<p3-p1> = (u3-u1)*U3d + (v3-v1)*V3d

These can be solved for the “basis” vectors, U3d and V3d to give:

U3d = ((v3-v1)<p2-p1> - (v2-v1)<p3-p1>) / ((u2-u1)(v3-v1) - (v2-v1)(u3-u1))
V3d = ((u3-u1)<p2-p1> - (u2-u1)<p3-p1>) / ((v2-v1)(u3-u1) - (u2-u1)(v3-v1))

These vectors have the correct directions to define a 3D local coordinate system but their lengths are not one. Therefore the vectors need to be normalized:

v_U3d = normalize(v_U3d);
v_V3d = normalize(v_V3d);

Using these vectors, the offsets from the bump map image can be applied to a normal vector. The “x offset” travels along the U3d axis and the “y offset” travels along the V3d axis. The new normal vector is calculated like this:

new_normal = normal + x_offset * U3d + y_offset * V3d;

This new_normal must be normalized because the lighting calculations expect a normal vector of unit length.

In summary, the offsets retrieved from the bump map image are applied to the normal vector relative to the triangle’s local coordinate system. To calculate the local coordinate system all of the vertices of the triangle and all of the texture coordinates of the triangle must be accessible. There are two scenarios:

If a model’s geometry and texture coordinates never change, pre-calculate the U3d and V3d vectors and store them in a GPU buffer object on a per vertex basis. This requires memory for 6 extra floats per vertex.
If a model’s geometry or texture coordinates are modified during rendering, the U3d and V3d vectors must be calculated in the vertex shader or the fragment shader during rendering. This requires that extra GPU buffer objects be created to store the other two vertices and the other two texture coordinates for the current triangle vertex. This requires 10 extra floats per vertex.

Caveat

It should be noted that the vectors N, U3d and V3d are typically not orthogonal and do not define a precise coordinate system (which requires that coordinate axes be 90 degrees apart). However, this is OK because we never use the three vectors to form an actual coordinate system.

An Example WebGL Program¶

The following WebGL program stores two extra vertices and two extra texture coordinates for each vertex and calculates a “local coordinate system” for each triangle vertex in the vertex shader. The U3d and V3d vectors are placed into varying variables so they are available to the fragment shader. Please experiment with the program and study the shader program. Please note that all of the lighting calculations are performed in “camera space” and therefore the U3d and V3d vectors must be converted to “camera space” as well (lines 76-77 in th vertex shader).

Make sure you investigate the difference between using an image as the source for surface colors vs. modifying the surface normals. You can change the WebGL program rendering below under the “Model Properties” options.

Show: Code Canvas Run Info

bump_map.vert
bump_map.frag

// Vertex Shader
precision mediump int;
precision mediump float;

// Scene transformations
uniform mat4 u_To_clipping_space; // Projection, camera, model transform
uniform mat4 u_To_camera_space;   // Camera, model transform

// Light model
uniform vec3  u_Light_position;
uniform vec3  u_Light_color;
uniform float u_Shininess;
uniform vec3  u_Ambient_intensities;

// The texture unit to use for the bump map
uniform sampler2D u_Texture_unit;

// Original model data
attribute vec3 a_Vertex;
attribute vec3 a_Color;
attribute vec3 a_Normal;
attribute vec2 a_Texture_coordinate;

// Bump map data to calculate a triangle's local coordinate system
attribute vec3 a_P2;
attribute vec3 a_P3;
attribute vec2 a_Uv2;
attribute vec2 a_Uv3;

// Data (to be interpolated) that is passed on to the fragment shader
varying vec3 v_Vertex;
varying vec4 v_Color;
varying vec3 v_Normal;

// Data (to be interpolated) that is passed on to the fragment shader
varying vec2 v_Texture_coordinate;

// The U, V texture coordinate axes in 3D space;
// That is, a local coordinate system for a triangle
varying vec3 v_U3d;
varying vec3 v_V3d;

//-------------------------------------------------------------------------
// Calculate the local coordinate system for this vertex's triangle
void calulate_triangle_coordinate_system(vec3 p1,  vec3 p2,  vec3 p3,
                                         vec2 uv1, vec2 uv2, vec2 uv3) {
  float u1 = uv1[0];
  float v1 = uv1[1];
  float u2 = uv2[0];
  float v2 = uv2[1];
  float u3 = uv3[0];
  float v3 = uv3[1];

float divisor = (u3-u1)*(v2-v1) - (u2-u1)*(v3-v1);

v_U3d = ((v2-v1)*(p3-p1) - (v3-v1)*(p2-p1)) /  divisor;
  v_V3d = ((u2-u1)*(p3-p1) - (u3-u1)*(p2-p1)) / -divisor;

normalize(v_U3d);
  normalize(v_V3d);
}

//-------------------------------------------------------------------------
void main() {

calulate_triangle_coordinate_system(a_Vertex, a_P2, a_P3,
                                      a_Texture_coordinate, a_Uv2, a_Uv3);

// Put the vertex's location into camera space.
  v_Vertex = vec3( u_To_camera_space * vec4(a_Vertex, 1.0) );

// Put the vertex's normal vector into camera space.
  v_Normal = vec3( u_To_camera_space * vec4(a_Normal, 0.0) );

// Put triangle's local coordinate system into camera space
  v_U3d = vec3( u_To_camera_space * vec4(v_U3d, 0.0) );
  v_V3d = vec3( u_To_camera_space * vec4(v_V3d, 0.0) );

// Pass the vertex's color to the fragment shader.
  v_Color = vec4(a_Color, 1.0);

// Pass the vertex's texture coordinate to the fragment shader.
  v_Texture_coordinate = a_Texture_coordinate;

// Transform the location of the vertex for the graphics pipeline.
  gl_Position = u_To_clipping_space * vec4(a_Vertex, 1.0);
}

// Fragment shader program
precision mediump int;
precision mediump float;

// The texture unit to use for the color lookup
uniform sampler2D u_Texture_unit;

// The dimensions of the bump map image: (width, height)
uniform vec2 u_Image_size;

// Fragment data
varying vec3 v_Vertex;
varying vec4 v_Color;
varying vec3 v_Normal;

// Bump map data for the fragment shader to calculate a triangle's
// local coordinate system
varying vec3 v_U3d, v_V3d;

// Data coming from the vertex shader
varying vec2 v_Texture_coordinate;

// Lighting model
uniform vec3  u_Light_position;
uniform vec3  u_Light_color;
uniform vec3  u_Ambient_intensities;

// Model surfaces' shininess
uniform float u_Shininess;

// Rendering options
uniform float u_Render_mode;
const float RENDER_BUMP_MAP = 1.0;
const float RENDER_COLORS   = 0.0;

//-------------------------------------------------------------------------
// Given texture coordinates, calculate the "finite difference"
// between neighboring pixels.
vec2 get_normal_offsets(vec2 texture_coordinates) {
  float pixel_delta_u = 1.0 / u_Image_size[0];
  float pixel_delta_v = 1.0 / u_Image_size[1];

vec2 up    = vec2(0.0,  pixel_delta_v);
  vec2 down  = vec2(0.0, -pixel_delta_v);
  vec2 left  = vec2(-pixel_delta_u, 0.0);
  vec2 right = vec2( pixel_delta_u, 0.0);

vec4 right_color = texture2D(u_Texture_unit, texture_coordinates + right);
  vec4 left_color  = texture2D(u_Texture_unit, texture_coordinates + left);
  vec4 up_color    = texture2D(u_Texture_unit, texture_coordinates + up);
  vec4 down_color  = texture2D(u_Texture_unit, texture_coordinates + down);

return vec2(right_color[0] - left_color[0], up_color[0] - down_color[0]);
}

//-------------------------------------------------------------------------
// Given a normal vector and texture coordinates, "bump" the
// normal vector based on the offsets from the bump texture map.
vec3 bump_map_normal(vec3 normal, vec2 texture_coordinates) {
  vec2 offsets = get_normal_offsets(texture_coordinates);
  normal = normal + offsets[0] * v_U3d + offsets[1] * v_V3d;
  return normalize(normal);
}

//-------------------------------------------------------------------------
// Given a normal vector and a light,
// calculate the fragment's color using diffuse and specular lighting.
vec3 light_calculations(vec3 fragment_color,
                        vec3 fragment_normal,
                        vec3 light_position,
                        vec3 light_color) {

vec3 specular_color;
  vec3 diffuse_color;
  vec3 to_light;
  vec3 reflection;
  vec3 to_camera;
  float cos_angle;
  float attenuation;
  vec3 color;

//- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  // General calculations needed for both specular and diffuse lighting

// Calculate a vector from the fragment location to the light source
  to_light = light_position - v_Vertex;
  to_light = normalize( to_light );

//- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  // DIFFUSE  calculations

// Calculate the cosine of the angle between the vertex's normal
  // vector and the vector going to the light.
  cos_angle = dot(fragment_normal, to_light);
  cos_angle = clamp(cos_angle, 0.0, 1.0);

// Scale the color of this fragment based on its angle to the light.
  diffuse_color = vec3(fragment_color) * light_color * cos_angle;

//- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  // SPECULAR  calculations

// Calculate the reflection vector
  reflection = 2.0 * dot(fragment_normal,to_light) * fragment_normal - to_light;
  reflection = normalize( reflection );

// Calculate a vector from the fragment location to the camera.
  // The camera is at the origin, so just negate the fragment location
  to_camera = -1.0 * v_Vertex;
  to_camera = normalize( to_camera );

// Calculate the cosine of the angle between the reflection vector
  // and the vector going to the camera.
  cos_angle = dot(reflection, to_camera);
  cos_angle = clamp(cos_angle, 0.0, 1.0);
  cos_angle = pow(cos_angle, u_Shininess);

// If this fragment gets a specular reflection, use the light's color,
  // otherwise use the objects's color
  specular_color = light_color * cos_angle;

color = diffuse_color + specular_color;
  color = clamp(color, 0.0, 1.0);

return color;
}

//-------------------------------------------------------------------------
void main() {

vec3 color, normal;

if (u_Render_mode == RENDER_BUMP_MAP) {
    // Modify the frament normal vector using the bump map image data.
    normal = bump_map_normal(v_Normal, v_Texture_coordinate);

// Perform the lighting calculations.
    color = light_calculations(vec3(v_Color), normal, u_Light_position, u_Light_color);

// Add in the ambient light
    color = color + u_Ambient_intensities * vec3(v_Color);

} else { // u_Render_mode == RENDER_COLOR_MAP
    vec4 frag_color = texture2D(u_Texture_unit, v_Texture_coordinate);

// Perform the lighting calculations.
    color = light_calculations(vec3(frag_color), v_Normal, u_Light_position, u_Light_color);

// Add in the ambient light
    color = color + u_Ambient_intensities * vec3(frag_color);
  }

gl_FragColor = vec4(color, 1.0);
}

Experiment with a Bump Map

Virtual World Bump mapped cube

camera eye (0.0, 0.0, 5.0)	camera center (0.0, 0.0, 0.0)
X: -5.0 +5.0	X: -5.0 +5.0
Y: -5.0 +5.0	Y: -5.0 +5.0
Z: -5.0 +5.0	Z: -5.0 +5.0

light position(3.0, 0.0, 5.0)	light color (1.00, 1.00, 1.00)
X: -5.0 +5.0	Red:	0.0 1.0
Y: -5.0 +5.0	Green:	0.0 1.0
Z: -5.0 +5.0	Blue:	0.0 1.0

ambient intensities (0.30, 0.30, 0.30)
Red:	0.0 1.0
Green:	0.0 1.0
Blue:	0.0 1.0
Change all intensities at once.

shininess = 30.0
0.1 128.0
Use the bump map image to modify the normal vectors. Use the bump map image for the surface color.

Show: Process information Warnings Errors

Open this webgl program in a new tab or window

Using Gimp to Create Bump Maps¶

Gimp includes tools for creating bump maps. One such tool is the emboss tool (Filters –> Distorts –> Emboss). The tool only works on color images. The WebGL program above uses an example image from Gimp’s documentation. The original color image is shown below, along with the results of changing the image size to a power of 2 and applying the embossing tool.

Original color image	“Embossed” image

Do a web search for “creating bump maps using Gimp” to learn further techniques and details on bump map creation.

Normal Maps¶

An image and its
associated normal map (1)

A normal map is a variation on bump maps. The RGB values in a normal map image are not used to modify a normal vector - they are the normal vector! An RGB pixel value, (red,green,blue), is used as a <dx,dy,dz> normal vector. The normal map is defined in the X-Y plane with the +Z axis being the general direction of the surface normal. Since the color (0,0,1) is blue, normal map images tend to be “blueish” in color, as in the example image to the right.

Normal vectors can point in any direction, but image color components are always positive values in the range [0.0, 1.0]. Therefore, normal vectors have to be transformed before they can be stored in an image. Given a normal vector component value in the range [-1.0, 1.0], it is scale by 1/2 and then offset by 1/2 to get it in the range [0.0, 1.0] (e.g, component*0.5 + 0.5). When a color is extracted from the image, each component must be converted back into a normal vector value by undoing the transformation, i.e., component*2.0 - 1.0.

Transforming Normal Vectors into “Triangle Space”¶

As with bump maps, normal map vectors must be transformed so they are relative to the surface they are modeling. Using the equations developed above for bump maps, the vectors U3d and V3d, along with a vertex’s normal vector N, can be used to create a local coordinate system for that vertex. A coordinate system is defined by 3 orthogonal vectors, so the three vectors must be made orthogonal. This can be done by taking the cross-product of two of the vectors to calculate the third vector. The order that you perform the cross-products determines the exact orientation of the coordinate system. Here are two possible scenarios:

Assume the normal vector should be orthogonal to the triangle’s surface:
- The vectors U3d and V3d line on the triangle’s surface, so cross(U3d, V3d) calculates N.
- Since N was calculated using a cross-product, it must be orthogonal to both U3d and V3d. Therefore, the only other operation required is to get U3d and V3d orthogonal. This can be done using either V3d = cross(N, U3d) or U3d = cross(V3d, N).
Assume the normal vector is for smooth shading and that it is not orthogonal to the triangle’s surface:
- N should not be changed, so recalculate both U3d and V3d to make them orthogonal.
- V3d = cross(N, U3d)
- U3d = cross(V3d, N)

We now have a valid coordinate system defined by the vectors U3d, V3d, and N. In lesson 7.6 you learned that a transformation matrix to position and orient a model in 3D space can be easily created from the model’s local coordinate system. The vectors that define the coordinate system are the columns of the transformation matrix:

ux
uy
uz
0
vx
vy
vz
0
nx
ny
nz
0
0
0
0
1
Eq1

Since we are transforming vectors which have direction but no location, the 4th row and column are not needed. Therefore, the following matrix will transform a vector defined in “global 3D space” into a triangle’s local coordinate space:

U3dx
U3dy
U3dz
V3dx
V3dy
V3dz
Nx
Ny
Nz
Eq2

In GLSL, a mat3 data type defines a 3-by-3 matrix defined in column-major order. Therefore, a transformation matrix can be created easily with this statement:

v_Local_coordinate_system = mat3(U3d, V3d, N);

Normal Maps in a Fragment Shader¶

The following fragment shader statements perform the required normal map calculations. Notice that the vector is retrieved from the normal map image, transformed into the orientation of the current 3D triangle, and then transformed into camera space for lighting calculations.

// Get the normal vector from the "normal map"
normal = vec3(texture2D(u_Texture_unit, v_Texture_coordinate));

// Transform the component values from [0.0,1.0] to [-1.0,+1.0]
normal = normal * 2.0 - 1.0;

// Transform the normal vector based on the triangle's
// local coordinate system
normal = v_Local_coordinate_system * normal;

// Transform the normal vector into camera space for the
// lighting calculations.
normal = vec3(u_To_camera_space * vec4(normal, 0.0) );

// Perform the lighting calculations.
color = light_calculations(vec3(v_Color), normal,
                           u_Light_position, u_Light_color);

// Add in the ambient light
color = color + u_Ambient_intensities * vec3(v_Color);

A WebGL Normal Map Program¶

Please experiment with the following program and study the shader programs.

Show: Code Canvas Run Info

normal_map.vert
normal_map.frag