Rotation Equations¶

To rotate a point, (x,y) about the origin beta degrees to a new location, (x_new,y_new), the point is moved as shown in the following diagram.

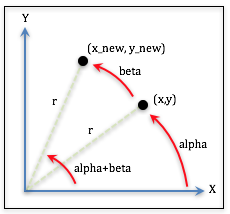
Rotate (x,y) beta degrees to (x_new,y_new)

From basic trigonometry, we know the following facts:

x = cos(alpha) * r              Eq1
y = sin(alpha) * r              Eq2

x_new = cos(alpha+beta) * r     Eq3
y_new = sin(alpha+beta) * r     Eq4

Using the “angle addition” formulas from trigonometry,

sin(alpha+beta) = sin(alpha)*cos(beta) + sin(beta)*cos(alpha)
cos(alpha+beta) = cos(alpha)*cos(beta) - sin(beta)*sin(alpha)

we can re-write equations 3 and 4 like this:

x_new = cos(alpha+beta) * r = [cos(alpha)*cos(beta) - sin(beta)*sin(alpha)] * r
y_new = sin(alpha+beta) * r = [sin(alpha)*cos(beta) + sin(beta)*cos(alpha)] * r

Multiplying r times each term and re-arranging gives us this:

x_new = cos(alpha)*r *cos(beta) - sin(beta) * sin(alpha)*r
y_new = sin(alpha)*r *cos(beta) + sin(beta) * cos(alpha)*r

Now, substituting equations 1 and 2 into these equations gives:

x_new = x * cos(beta) - sin(beta) * y
y_new = y * cos(beta) + sin(beta) * x

Writing this in matrix format gives:

This is a rotation about the Z axis. The z component of a 3D vertex is not effected by this rotation, so we can write the rotation in terms of a 3D transformation matrix like this:

Using similar logic, rotations about the X and Y axes can be easily formulated.