11.1 - Introduction to Surface Properties¶
Your eyes “see” an object because light has reflected from the object into your eye. The properties of a surface affect how light reflects from a surface. This chapter discusses how to model the properties of surfaces.
Overview of Lessons¶
In the previous chapter you learned how to model light and its reflection from surfaces. Isn’t it amazing how much better the renderings looked when the color of the pixels was based on reflected light! However, all of the previous WebGL programs used a single color to represent a surface’s appearance. This causes the surfaces to appear too uniform and “pure.” Real-world objects have more variation over their surfaces. If the surface properties of a model’s triangular mesh are modeled accurately we can approach photo-realism in CGI renderings. (To get exact “photo-realism” you typically need advanced algorithms such as ray tracing and a radiosity lighting model which are beyond the scope of this textbook.)
Surface properties are complex and we can’t cover them all here. However, we will cover the basics:
| Surface Property | Description |
|---|---|
| Color | The color of a surface is actually not a single color, but a set of colors because a surface reacts differently to ambient, diffuse and specular light reflection. |
| Flat vs. Curved | WebGL only renders triangles, but we can modify the normal vectors at a triangle’s vertices to simulate curved surfaces. |
| Texture | A surface can have multiple colors. A good example is a piece of clothing. |
| Smooth vs. Bumpy | A surface can be smooth or bumpy across its surface. |
| Shiny vs. Dull | A surface might be irregular at a microscope level and appear “dull” because it reflects light in all directions, even for specular reflection. Or it might be very smooth at a microscope level and specular reflection has minimal scattering. |
These properties can be simulated using data, using algorithms, or a combination of the two. We will discuss all three techniques.
Managing the Data¶
Surface properties for a model can be uniform across all surfaces OR
the surface properties can vary for each triangle of a triangular mesh.
If the surface properties are uniform, the data will be passed to a
shader program using uniform variables. If the surface properties
are different for each triangle, the data must be stored “per vertex” in
a GPU object buffer and accessed using attribute variables.
Surface Property Transformations¶
As in the previous chapter, surface calculations will be performed in “camera space” because:
- The GPU shader program knows the camera’s location and orientation
without updating any
uniformvariables. (The camera is at the global origin and aligned with the global axes.) - Some calculations are simplified with the camera being at the origin.
Therefore, any surface properties that are related to the location or orientation of a model must be transformed into “camera space.” This is straightforward in most cases, but problematic if your transformation includes non-uniform scaling. Note that a camera transformation never includes scaling – only rotation and translation. So the problem arises if your model transformations includes non-uniform scaling.
Reminder
Uniform scaling occurs when the scale factors for each axis are identical, such
as matrix.scale(transform, 3,3,3). Non-uniform scaling occurs
when the scale factors are not identical, such as matrix.scale(transform, 3,1,3).
No Scaling or Uniform Scaling¶
If your model transformation includes translation, rotation, and/or uniform
scaling, you can use your camera-model transformation to convert a model’s
normal vectors into “camera space”. Vectors have no location,
only magnitude and direction. Therefore, a vector’s
homogeneous coordinate must be zero so it can’t be translated.
The vector <dx,dy,dz> becomes <dx,dy,dz,0> before being
multiplied by the camera-model transformation. (As a general rule, never use a
projection-camera-model transformation on model normal vectors.)
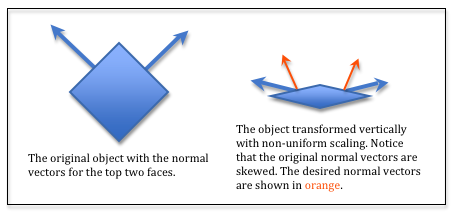
Non-uniform scaling.
Non-uniform scaling¶
Consider the diagram to the right. If you transform a model using non-uniform scaling, the normal vectors become skewed and no longer point in the correct direction. This simple example shows that the model transformation used on the vertices of a model will produce invalid normal vectors in scene space.
Non-uniform scaling.
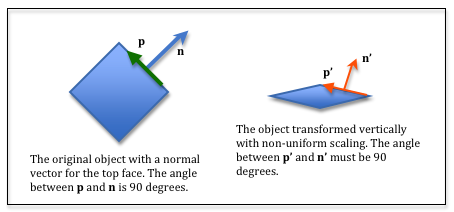
Let’s derive a transformation that will transform the normal vectors
correctly – assuming non-uniform scaling has been applied to a model.
In the diagram to the right, assume that the vector, p, lies
in the plane defined by the top face. The angle between p
and the face’s normal vector, n, must be 90 degrees. Therefore, the
dot product of p and n, must be zero. That is,
dot_product(p,n) === 0.
Let M be the transformation that contained the non-uniform scaling of
the model. Therefore p' = M * p. We need to solve for a different
transformation, S, that will transform n into n' such that
dot_product(p',n') === 0. Therefore, dot_product(M * p, S * n) === 0.
You can reorder the multiplication of a matrix times a vector by taking the transpose of each one like this:
e
i
m
b
f
j
n
c
g
k
o
d
h
l
p
*x
y
z
0
=x
y
z
0
*a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
p
Eq2
MT * S === I(MT) -1 * MT * S === (MT) -1 * IS === (MT) -1S === (M-1) T (See the matrix identities below.)
Summary¶
If a model transformation uses non-uniform scaling, your JavaScript code must create three separate transformations for a model rendering:
- A camera-model transformation to transform the model’s vertices into “camera space”.
- A camera-model inverse-transposed transformation to transform the model’s normal vectors into “camera space”.
- A projection-camera-model transformation to transform a model’s vertices into clipping-space.
For the remainder of these tutorials we will assume that model transformations contain no scaling (or only uniform scaling). Therefore, the special matrix (M-1) T will not be needed.
Glossary¶
- surface properties
- Characteristics of a triangle that determines how light is reflected from its surface.
Basic Matrix Identities¶
The following properties of matrix operations are true (1), where A and B are square matrices, AT is the transpose of A, and A-1 is the inverse of A.
- (A*B)T = BT * AT
- (AT)T = A
- (A+B)T = AT + BT
- (A*B)-1 = B-1 * A-1
- (AT)-1 = (A-1)T
Self Assessment¶
- color.
- Correct.
- roughness
- Correct.
- curvature
- Correct.
- patterns (or texture)
- Correct.
Q-241: Which of the follow are surface properties that can be modeled? (Select all that apply.)
uniform- Correct.
attribute-
Incorrect.
attributevariables hold data that is different for each vertex. varying-
Incorrect.
varyingvariables hold data that is interpolated between the vertices that define a geometric primitive (i.e., point, line, triangle). - global constant
-
Not the preferred answer, but technically correct. However, this makes
the shader program more specific and perhaps not usable in other scenes.
Making the data
uniformallows a JavaScript program to “tweak” rendering parameters at run-time.
Q-242: If a surface property is the same for all triangles in a polygonal mesh, the data used to model the surface property is typically stored in what type of shader program variable?
matrix.scale(transform, 0.5, 0.6, 0.7)- Correct. The three scale factors are not identical.
matrix.scale(transform, 1.0, 1.0, 1.0)- Incorrect. This does uniform scaling, but actually no scaling since the factors are all 1.0.
matrix.scale(transform, 4.0, 4.0, 4.0)- Incorrect. This does uniform scaling.
matrix.scale(transform, 0.6, 0.6, 0.6)- Incorrect. This does uniform scaling.
Q-243: Which of the following commands creates a non-uniform scaling transformation matrix?
- when the transformation matrix includes non-uniform scaling.
- Correct.
- when the camera transformation matrix includes non-uniform scaling.
- Incorrect. A camera transformation matrix contains only translation and rotation, never scaling.
- when the transformation matrix includes any type of scaling.
- Incorrect. Uniform scaling is fine. Only when non-uniform scaling is included is the special matrix, (M-1)T, required.
- when the transformation matrix includes uniform scaling.
- Incorrect. Uniform scaling is fine. Only when non-uniform scaling is included is the special matrix, (M-1)T, required.
Q-244: When is the transpose of the inverse of a transformation matrix, (M-1)T required for the correct placement of normal vectors into a scene?