9.3 - Perspective Projections¶
Perspective projections render a virtual scene to make it appear like a view from a real-world camera. Objects further from the camera appear to be smaller and all lines appear to project toward vanishing points which skew parallel lines. Perspective projections are almost always used in gaming, movie special effects, and scientific visualizations.
This lesson describes how to create a perspective projection. The following lesson explains its mathematics.
The Viewing Volume of a Perspective Projection¶

(Source 1)
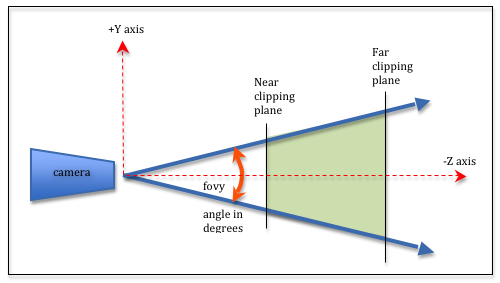
A perspective projection defines a 3D volume that projects out from the location of the camera along four boundary rays. The rays form a viewing frustum as shown in the image to the right. The frustum includes a front and back clipping plane that is parallel to the X-Y plane. Any models inside this viewing frustum will be rendered. Any models outside this viewing frustum will be clipped away.
There are two standard ways to define a viewing frustum.
- The
createPerspective()function simulates the lens of a camera that is always at the global origin looking down the -Z axis. - The
createFrustum()function defines a 2D viewing window that is parallel to the X-Y plane. The camera can be located anywhere in the X-Y plane, but is always looking down a ray that is parallel to the -Z axis. A common use of this function is to render two different views of a scene, one for a user’s left eye and another for a user’s right eye. If the two renderings are offset correctly, and displayed to a user’s individual eyes, the user can see a 3D scene! This is how virtual reality (VR) is created.
Please study these two methods for creating perspective projections.
The createPerspective() function¶
The function createPerspective() in the Learn_webgl_matrix.js
module creates a perspective projection transformation matrix. The
function requires 4 parameters as shown in its function prototype below.
/** -----------------------------------------------------------------
* Create a perspective projection matrix using a field-of-view and an aspect ratio.
* @param fovy {Number} The angle between the upper and lower sides of the viewing frustum.
* @param aspect {Number} The aspect ratio of the view window. (width/height).
* @param near {Number} Distance to the near clipping plane along the -Z axis.
* @param far {Number} Distance to the far clipping plane along the -Z axis.
* @return {Float32Array} The perspective transformation matrix.
*/
self.createPerspective = function (fovy, aspect, near, far)
The four parameters define a frustum. The fovy parameter stands
for the “field of view y-axis” and is the vertical angle of the camera’s lens.
Common values for fovy range from 30 to 60 degrees. The aspect
ratio parameter
is the width divided by the height of the canvas window.
The near and far parameters are distances from the camera,
with the restriction that near is always less than far and both
distances must always be positive. The distance between
near and far should be kept as small as possible to reduce precision
issues since the frustum is being mapped into a clipping volume
that is 2 units deep. Typical values for near and far might be
0.1 to 100.0. In general, make near be as far away from the camera as
possible and make far be as close to the camera as possible.
Experiment with the parameters using the following WebGL program.
Experiment with an Perspective Projection
Manipulate parameters of createPerspective(fovy, aspect, near, far):
| fovy (field-of-view y axis) : | 45 degrees | 5.0 179 |
|
aspect ratio (width/height) : Change canvas size to match aspect ratio. |
1.0 | 0.1 5.0 |
| near : | 2.0 | 0.1 10.0 |
| far : | 10.0 | 2.0 20.0 |
Open this webgl demo program in a new tab or window
As you experiment with the perspective parameters, please verify that you understand the following ideas:
- As the angle for the camera’s lens,
fovy, gets smaller, the objects in the scene get larger. This is consistent with how light travels through the optics of a camera. - If the
aspectratio changes but the canvas remains unchanged, the rendering will be distorted. It is the programmer’s job to insure the aspect ratio of the perspective matches the aspect ratio of the canvas. - The value of
nearhas no impact on the rendered view. It does affect what is clipped from the scene. The same is true for the value offar. - The
nearandfarparameters are always positive andnearshould always be less thanfar. Thenearandfarparameters are both distances; they are not -Z axis locations.
The createFrustum() function¶
The function createFrustum() in the GlMatrix4x4.js
module creates a perspective projection transformation matrix. The
function requires 6 parameters as shown in its function prototype below.
/** -----------------------------------------------------------------
* Create a perspective projection matrix based on the limits of a frustum.
* @param left {Number} Farthest left on the x-axis
* @param right {Number} Farthest right on the x-axis
* @param bottom {Number} Farthest down on the y-axis
* @param top {Number} Farthest up on the y-axis
* @param near {Number} Distance to the near clipping plane along the -Z axis
* @param far {Number} Distance to the far clipping plane along the -Z axis
* @return {Float32Array} A perspective transformation matrix
*/
self.createFrustum = function (left, right, bottom, top, near, far)
The 3D points (left, bottom, near) and (right, top, near) define the lower-left
and upper-right corners of the viewing window. If you calculate the center
of the viewing window and cast this point back to the X-Y plane, this point
is the apex of the frustum. Casting rays from the apex through the
four points of the viewing window forms the frustum. (The location of the
apex is displayed in the demo below as a small black dot.) Remember that the
camera is at the origin looking down the -Z axis. (The camera is not rendered
so that you can see the apex location of the frustum.)
Experiment with the parameters using the following demo.
Experiment with an Perspective (frustum) Projection
Manipulate parameters of createFrustum(left, right, bottom, top, near, far):
| left : | -2.0 | -5.0 5.0 | right : | 2.0 | -5.0 5.0 |
| bottom : | -2.0 | -5.0 5.0 | top : | 2.0 | -5.0 5.0 |
| near : | 3.0 | 1.0 10.0 | far : | 10.0 | 2.0 15.0 |
Open this webgl demo program in a new tab or window
As you experiment with the frustum parameters, please verify that you understand the following ideas:
createFrustumallows you to create a frustum that is “off center” from the -Z axis, but its field of view is always parallel to the -Z axis.- It is the programmer’s job to insure that the canvas dimensions have an aspect ratio (width/height) that is consistent with the aspect ratio of the viewing window (right-left)/(top-bottom). If the aspect ratios are different, the rendering is distorted.
- Changing the value of
nearhas a profound effect on the frustum because this is the distance from the camera to the viewing window and the entire frustum is defined by the corners of the viewing window. Changing thenearvalue changes the camera lens’ field-of-view (.i.e.,fovy). - Changing the value of
faronly affects clipping. - If the values of
leftandrightare not symmetrical about the origin, the apex of the frustum moves horizontally away from the origin. - If the values of
topandbottomare not symmetrical about the origin, the apex of the frustum moves vertically away from the origin.
createPerspective() vs. createFrustum()¶
How are createPerspective() and createFrustum() similar?
- Both create a perspective transformation matrix that maps a frustum shaped virtual world into normalized device coordinates.
How are they different?
- They require different parameters to define the frustum viewing volume.
- For
createPerspective(), the camera is always at the origin, while forcreateFrustumthe camera can be offset from the global origin along the X or Y axis. - For
createPerspective(), the field-of-view is controlled by an angle,fovy, while forcreateFrustumthe field-of-view is controlled by thenearparameter, which defines how far the viewing window is from the camera.
To demonstrate the equivalence of the functions, the following two examples show how you could use one function to implement the other one.
function createPerspectiveUsingFrustum (fovy, aspect, near, far) {
let top, bottom, left, right;
top = near * Math.tan(toRadians(fovy)/2);
bottom = -top;
right = top * aspect;
left = -right;
return createFrustum(left, right, bottom, top, near, far);
}
function createFrustumUsingPerspective (left, right, bottom, top, near, far) {
let fovy, aspect;
fovy = 2 * toDegrees(Math.atan2(top, near));
if (-left === right && -bottom === top ) {
// The camera is at the origin
aspect = right / top; // width / height
return createPerspective(fovy, aspect, near, far);
} else {
// The camera is not at the origin, so createPerspective will not work.
return ERROR;
}
}
Stereo Vision¶
Virtual reality and augmented reality applications render two different scenes for a user, one for the left eye and one for the right eye. If each eye of a user only sees their respective image, the user’s brain perceives a real 3D scene. There are two standard ways to get a user’s eyes to see the correct image: 1) VR goggles have a screen in front of each eye, or 2) polarized glasses filter a single image into two separate images.
Experiment with the following WebGL program which renders two images of the same scene, but with the camera for each scene offset from the origin.
Experiment with Stereo Projections
|
Left eye's view:
(frustum shown in red) |
Right eye's view:
(frustum shown in green) |
| Distance between projections : | 0.4 | 0.0 4.0 |
| left : | -2.0 | -5.0 5.0 | right : | 2.0 | -5.0 5.0 |
| bottom : | -2.0 | -5.0 5.0 | top : | 2.0 | -5.0 5.0 |
| near : | 3.0 | 1.0 10.0 | far : | 10.0 | 2.0 15.0 |
Open this webgl demo program in a new tab or window
Please notice that if the two images were in a headset where each eye only saw its projection, each eye sees a different rendering of the objects, but your brain sees a single 3D version of each object (assuming the distance between the projections is approximately the same distance between your eyes). Amazing!!!!
Glossary¶
- projection
- Transform the vertices of a 3D model into 2D points on a 2D viewing window. And prepare the 3D data for the next stages of the graphics pipeline.
- perspective projection
- The location of every 3D vertex is projected straight to the location of the camera. This produces a rendering in the same way a human’s eyes receives light from the real world.
- frustum
- The portion of a pyramid that lies between two parallel cutting planes.
- virtual reality
- A person is shown a separate image to each eye and perceives a 3D scene, not a 2D image.