9.1 - Introduction to Projections¶

Clipping¶

When you point a real camera at something to take a picture, only a portion of the real-world is visible in the camera’s field-of-view. The same is true of the human eye; you only see what is in front of you. We want the same behavior for our virtual scenes. The process of determining what is visible and what is not visible is called clipping. Clipping is done automatically by WegGL. However, to make clipping as efficient as possible, clipping is always done inside a cube centered at the origin.

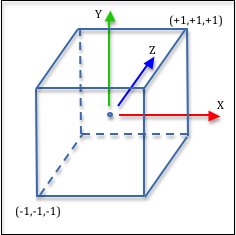
The clipping volume is a 2 unit wide cube, with the X axis going from -1 to +1, the Y axis going from -1 to +1, and the Z axis going from -1 to +1, as shown in the image to the right. A scene that has been transformed to fit inside this clipping volume is said to be defined in Normalized Device Coordinates (NDC).

Did you notice that the clipping volume is defined in a left-handed coordinate system? The Z-axis is pointing into the page! Previous lessons have stated that WebGL always uses a right-handed coordinate system and now it doesn’t. What is going on? The designers of WebGL (i.e., OpenGL) believed that the “right-hand rule” for spacial orientation feels natural and comfortable for the majority of people, while the designers of graphics hardware wanted consistency of data. It is easy to reconcile these differences: for WebGL programs a projection is designed to invert the orientation of the coordinate system in preparation for GPU implemented functionality.

You can visually see the left-handed coordinate system of the GPU in the following demo program. Observe what happens when you include an projection matrix and when you don’t.

Given that the clipping volume uses a left-handed coordinate system, there are two very important implications to the WebGL graphics programmer:

• You must always include a projection matrix in your vertex transform, even if you don’t think you need one. All of the transformations we have defined previously assumed a right-handed coordinate system. If you don’t include a projection matrix, all of the other transformation matrices will not work correctly.
• If you create your own projection matrix, it must negate the z values of all vertices.

Clipping Algorithms¶

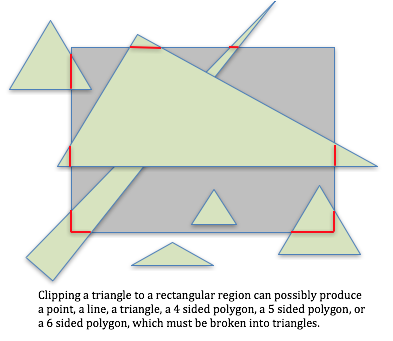
Clipping is a very difficult problem, as demonstrated by the image below. Clipping is one of the main reasons why WebGL only render points, lines and triangles. Clipping geometric primitives that are more complex than triangles is difficult and computationally expensive.

To better understand why clipping is done in normalized device coordinates, consider how clipping points might be done using programming logic. To determine if a point defined as (x,y,z) is inside the clipping volume, you might write code like this:

if (x >= -1 and x <= 1 and
    y >= -1 and y <= 1 and
    z >= -1 and z <= 1)
  point_is_visible = true;
else
  point_is_visible = false;

However, since the clipping volume is uniform and symmetrical about the origin, using an absolute value function simplifies this code to:

if (abs(x) <= 1 and abs(y) <= 1 and abs(z) <= 1)
     point_is_visible = true;
else
     point_is_visible = false;

Furthermore, you could set the boolean value with just a simple assignment like this:

point_is_visible = (abs(x) <= 1 and abs(y) <= 1 and abs(z) <= 1);

Actually clipping is done in homogeneous coordinates (which you will learn more about in a couple of lessons). For a (x,y,z,w) vertex, the clipping test would be

point_is_visible = (abs(x/w) <= 1 and abs(y/w) <= 1 and abs(z/w) <= 1)

// Or, remove the division for efficiency to get
point_is_visible = (abs(x) <= w and abs(y) <= w and abs(z) <= w)

Summary

A projection must map a virtual scene into normalized device coordinates to facilitate efficient clipping.

You should be very grateful that the graphics pipeline implements clipping for you because it is a complex problem to solve.

Viewport Mapping¶

After clipping, the (x,y) values of vertices must be mapped to pixel locations in a 2D image. Later in this chapter we will discuss the details of this viewport mapping.

Perspective Divide¶

Creating a perspective view of a virtual scene requires a division operation on each x, y, z, component of a vertex. This is accomplished by performing performing transformations in 4D space and using the w component of each vertex for a divisor. Later in this chapter we will discuss the details of the perspective divide operation.