8.5 - Bezier Parametric Equations — Learn Computer Graphics using WebGL

Speed and Acceleration¶

First, let’s review the definition of speed and acceleration in terms of calculus derivatives.

Speed is the change in location over a time interval, such as 30 miles per hour (or 30 mph). Calculus derivatives provide tools for measuring the “rate of change” of variables.

Speed defined using derivatives:

speed = Δ distance / Δ time

or

speed = d(distance) / dt

If you are rusty with your calculus derivatives, please review these basic derivative rules.

Let’s take the derivative of the parametric equation we used for basic motion, where p1 and p2 are constants.

p = (1-t)*p1 + t*p2;  // where t varies from 0.0 to 1.0

speed = d(p)/dt = d((1-t)*p1)/dt + d(t*p2)/dt = -p1 + p2 = p2 - p1

Interesting! The derivative of the equation produces the subtraction of two points, which is how we calculate a vector. This means that the motion defined by this equation over time is equal to a constant vector – which translates to a constant speed between the two points – because we are assuming that the “change in time” between each frame is constant and defined by the frame-rate.

Acceleration is the change in speed over a time interval. The derivative of the speed equation above is zero because p1 and p2 are constants.

acceleration = d(speed)/dt = d(p2 - p1)/dt = 0

Again this shows that the parametric equation calculates a constant speed over the interval – because there is no acceleration.

But what if we want more realistic motion that includes acceleration and deceleration instead of instantaneous movement.

Bezier Parametric Equations¶

Let’s define our path of motion using four points instead of two points. Let the four points be defined as follows:

p0 - the starting point of the path.
p1, p2 - intermediate points that influence the direction, speed and acceleration of the motion.
p3 - the ending point of the path.

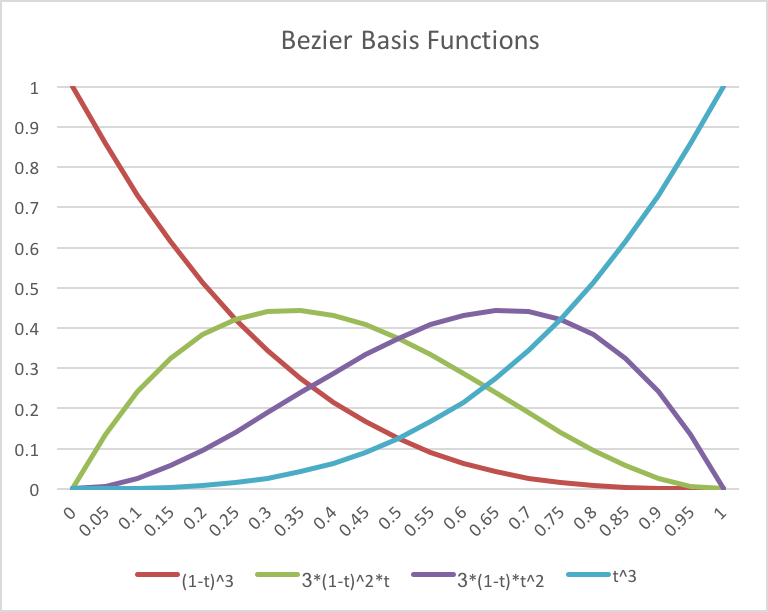
To create a “weighted sum” of these points we define four basis functions as follows:

p = (1-t)³ * p0 + 3*(1-t)²*t* p1 + 3*(1-t)*t²* p2 + t³* p3;

The basis functions calculate the percentage of contribution of each point and are plotted in the diagram to the right. The speed and acceleration at each location along the path is defined by the equation’s derivatives:

speed = d(p)/dt = 3*[(1-t)^2(p1-p0) + 2(1-t)(t)(p2-p1) + (t^2)(p3-p2)]
acceleration = d(speed)/dt = 6*[(-1+t)(p1-p0) + (1-2t)(p2-p1) + t(p3-p2)]

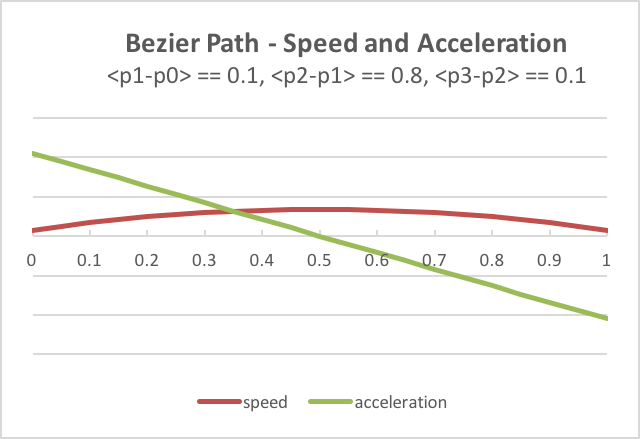
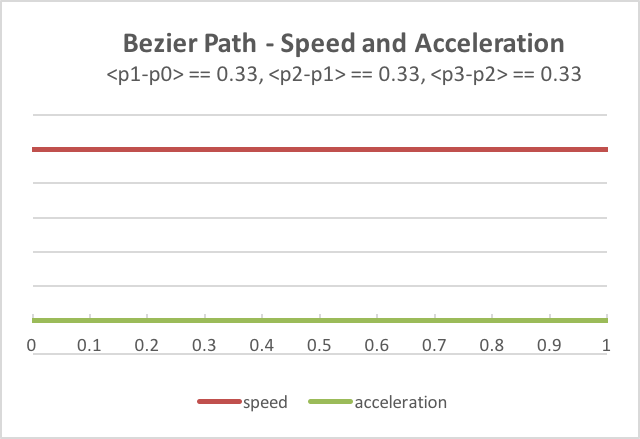
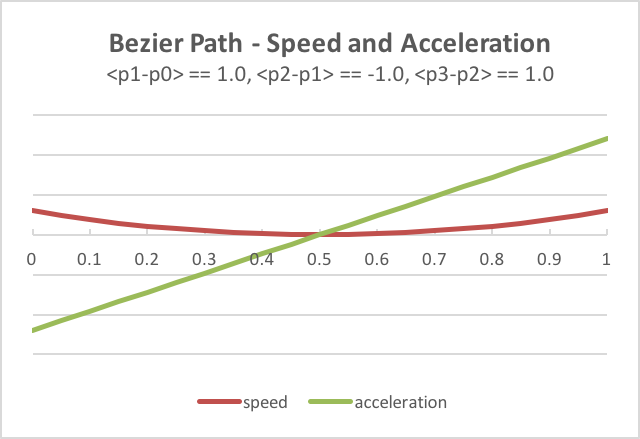
Notice that both the speed and the acceleration are functions of the three vectors defined by the four controls points. The speed and acceleration are the magnitude of these vectors and the direction of the vectors determines the direction of motion. (Remember that an animator is typically concerned with visual appearance and not exact speed or acceleration values.) To get a feeling for how the intermediate control points affect speed and acceleration, the following chart shows various scenarios as the location of the points are changed. You can visually see these results in the WebGL program below as you modify the scale factor for the <p1-p0> vector. Please verify that the visual motion of the model matches the speed and acceleration indicated in the charts.

`<p1-p0>` Scale Factor	Control Points and Vectors General Description of Motion	Speed and Acceleration Graph
0.0	`p0 == p1` `p2 == p3` The speed starts and ends at zero. The speed is maximum at the mid-point of the path.
0.1	`<p1-p0> = 0.1<p3-p0>` `<p3-p2> = 0.1<p3-p0>` Increasing the vector `<p1-p0>` decreases the overall speed and acceleration.
0.33333	`<p1-p0> = (1/3)<p3-p0>` `<p3-p2> = (1/3)<p3-p0>` Spacing the control points equally along the path makes the acceleration go to zero and you have constant speed over the path.
0.5	`p1 == p2` `<p2-p1> == 0` `<p1-p0> == <p3-p2>` Placing both intermediate points at the center of the path inverts the speed such that the minimum speed is at the path’s mid-point.
1.0	`p1 == p3` `p2 == p0` `<p2-p1> == -<p3-p0>` Placing the intermediate points at the opposite end-points of the path inverts the speed such that the speed goes to zero at the path’s mid-point.

Please experiment with the following WebGL program and verify that the visual results of the animations match the speed and acceleration charts shown above.

Show: Code Canvas Run Info

bezier_path.js
bezier_scene.js

/**
 * bezier_path.js, By Wayne Brown, Fall 2017
 */

/**
 * The MIT License (MIT)
 *
 * Copyright (c) 2015 C. Wayne Brown
 *
 * Permission is hereby granted, free of charge, to any person obtaining a copy
 * of this software and associated documentation files (the "Software"), to deal
 * in the Software without restriction, including without limitation the rights
 * to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
 * copies of the Software, and to permit persons to whom the Software is
 * furnished to do so, subject to the following conditions:
 *
 * The above copyright notice and this permission notice shall be included in all
 * copies or substantial portions of the Software.

* THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
 * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
 * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
 * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
 * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
 * OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
 * SOFTWARE.
 */

"use strict";

/**------------------------------------------------------------------------
 * Store and manipulate a path defined by 4 control points.
 * @param control_points {Array} of GlPoint4 locations
 * @param start_frame {number} the frame that starts the path animation
 * @param end_frame {number} the frame that ends the path animation
 * @constructor
 */
window.BezierPath = function (control_points, start_frame, end_frame) {

// Constructor
  let self = this;

// Objects needed for internal elements and calculations
  let P = new GlPoint4();

// The points that define the path
  let p0 = control_points[0];
  let p1 = control_points[1];
  let p2 = control_points[2];
  let p3 = control_points[3];

self.control_points = control_points;
  self.start_frame = start_frame;
  self.end_frame = end_frame;

// Calculate speed and acceleration for display purposes
  let p1_temp = P.create();
  let p2_temp = P.create();
  self.speeds = null;
  self.accelerations = null;

/**----------------------------------------------------------------------
   * Calculate an intermediate point along a straight path between P1 and P2.
   * @param p {GlPoint4} the result of the intermediate point calculation
   * @param frame {number} which frame of an animation
   */
  self.intermediatePoint = function (p, frame) {

let number_deltas, t, t0, t1, t2, t3;

if (frame <= self.start_frame) {
      P.copy(p, p0);
    } else if (frame >= self.end_frame) {
      P.copy(p, p3);
    } else {
      number_deltas = self.end_frame - self.start_frame;
      t = (frame - self.start_frame) / number_deltas;

t0 = Math.pow(1-t, 3);
      t1 = 3.0 * t * Math.pow(1-t, 2);
      t2 = 3.0 * Math.pow(t, 2) * (1-t);
      t3 = Math.pow(t, 3);

p[0] = t0 * p0[0] + t1 * p1[0] + t2 * p2[0] + t3 * p3[0];
      p[1] = t0 * p0[1] + t1 * p1[1] + t2 * p2[1] + t3 * p3[1];
      p[2] = t0 * p0[2] + t1 * p1[2] + t2 * p2[2] + t3 * p3[2];
    }
  };

/**----------------------------------------------------------------------
   * Calculate the speed and acceleration along the path.
   * This is for display purposes only - it is not needed to animate the path.
   * @param frame_rate {number} the number of frames per second.
   */
  self.calculateActualSpeeds = function (frame_rate) {

let which_frame = self.start_frame;
    let time_between_frames = 1.0 / frame_rate;

// Calculate the speeds and accelerations for display purposes only
    let number_frames = self.end_frame - self.start_frame + 1;
    self.speeds        = new Array(number_frames);
    self.accelerations = new Array(number_frames);

self.intermediatePoint(p1_temp, which_frame);
    self.speeds[0] = 0;

for (let index = 1; index < number_frames; index++) {
      which_frame += 1;
      self.intermediatePoint(p2_temp, which_frame);
      self.speeds[index] = P.distanceBetween(p1_temp, p2_temp) / time_between_frames;
      P.copy(p1_temp, p2_temp);
    }

self.accelerations[0] = 0;
    for (let index = 1; index < number_frames; index++) {
      self.accelerations[index] = (self.speeds[index] - self.speeds[index-1])
                                   / time_between_frames;
    }
  };

};

/**
 * bezier_scene.js, By Wayne Brown, Fall 2017
 */

/**
 * The MIT License (MIT)
 *
 * Copyright (c) 2015 C. Wayne Brown
 *
 * Permission is hereby granted, free of charge, to any person obtaining a copy
 * of this software and associated documentation files (the "Software"), to deal
 * in the Software without restriction, including without limitation the rights
 * to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
 * copies of the Software, and to permit persons to whom the Software is
 * furnished to do so, subject to the following conditions:
 *
 * The above copyright notice and this permission notice shall be included in all
 * copies or substantial portions of the Software.

* THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
 * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
 * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
 * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
 * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
 * OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
 * SOFTWARE.
 */

"use strict";

/** -----------------------------------------------------------------------
 * Create a WebGL 3D scene, store its state, and render its models.
 *
 * @param id {string} The id of the webglinteractive directive
 * @param download {SceneDownload} An instance of the SceneDownload class
 * @param vshaders_dictionary {object} A dictionary of vertex shaders.
 * @param fshaders_dictionary {object} A dictionary of fragment shaders.
 * @param models {object} A dictionary of models.
 * @constructor
 */
window.BezierScene = function (id, download, vshaders_dictionary,
                                fshaders_dictionary, models) {

// Private variables
  let self = this;
  let my_canvas = null;

let gl = null;
  let program = null;
  let textx, texty, textz, cubex, cubey, cubez, cube_center;
  let textx_gpu, texty_gpu, textz_gpu, cubex_gpu, cubey_gpu,
      cubez_gpu, cube_center_gpu;

let x_axis_gpu, y_axis_gpu, z_axis_gpu;
  let x_axis, y_axis, z_axis;

let sphere, sphere_gpu;

let matrix = new window.GlMatrix4x4();
  let translate = matrix.create();
  let transform = matrix.create();
  let projection;
  let camera = matrix.create();
  let rotate_x_matrix = matrix.create();
  let rotate_y_matrix = matrix.create();
  let scale_axes = matrix.create();
  let base = matrix.create();

let point_translate = matrix.create();
  let point_scale = matrix.create();
  matrix.scale(point_scale, 0.1, 0.1, 0.1);

// Public variables that will possibly be used or changed by event handlers.
  self.angle_x = 0.0;
  self.angle_y = 0.0;
  self.out = download.out;
  self.current_frame = 0;

// The points that define the path
  let P = new GlPoint4();
  self.control_points = [ P.create(-5, 0, 0),
                          P.create( -4, 0, 0),
                          P.create( 4, 0, 0),
                          P.create( 5, 0, 0) ];

self.path = new BezierPath(self.control_points, 30, 60);
  let p = P.create();

//-----------------------------------------------------------------------
  function _renderCubes(transform) {
    textx.render(transform);
    texty.render(transform);
    textz.render(transform);
    cubex.render(transform);
    cubey.render(transform);
    cubez.render(transform);
    cube_center.render(transform);
  }

//-----------------------------------------------------------------------
  self.render = function () {

// Build individual transforms
    matrix.setIdentity(transform);
    matrix.rotate(rotate_x_matrix, self.angle_x, 1, 0, 0);
    matrix.rotate(rotate_y_matrix, self.angle_y, 0, 1, 0);
    matrix.multiplySeries(base, projection, camera, rotate_x_matrix, rotate_y_matrix);

self.path.intermediatePoint(p, self.current_frame);
    matrix.translate(translate, p[0], p[1], p[2]);

// Render the cubes models
    matrix.multiplySeries(transform, base, translate);
    _renderCubes(transform);

// Render the global axes
    matrix.multiplySeries(transform, base, scale_axes);
    x_axis.render(transform);
    y_axis.render(transform);
    z_axis.render(transform);

//  - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
    // Render the control points on the bezier path
    for (let j=0; j<4; j++) {
      matrix.translate(point_translate, self.path.control_points[j][0],
                                        self.path.control_points[j][1],
                                        self.path.control_points[j][2]);
      matrix.multiplySeries(transform, base, point_translate, point_scale);
      sphere.render(transform);
    }
  };

//-----------------------------------------------------------------------
  self.delete = function () {

// Clean up shader programs
    gl.deleteShader(program.vShader);
    gl.deleteShader(program.fShader);
    gl.deleteProgram(program);

// Delete each model's VOB
    textx.delete(gl);
    texty.delete(gl);
    textz.delete(gl);
    cubex.delete(gl);
    cubey.delete(gl);
    cubez.delete(gl);
    cube_center.delete(gl);
    x_axis.delete(gl);
    y_axis.delete(gl);
    z_axis.delete(gl);

self.events.removeAllEventHandlers();
  };

//-----------------------------------------------------------------------
  // Object constructor. One-time initialization of the scene.

// Get the rendering context for the canvas
  my_canvas = download.getCanvas(id + "_canvas");  // by convention
  if (my_canvas) {
    gl = download.getWebglContext(my_canvas);
  }
  if (!gl) {
    return;
  }

// Set up the rendering program and set the state of webgl
  program = download.createProgram(gl, vshaders_dictionary["color_per_vertex"], fshaders_dictionary["color_per_vertex"]);

gl.useProgram(program);

gl.enable(gl.DEPTH_TEST);

gl.clearColor(0.98, 0.98, 0.98, 1.0);

projection = matrix.createPerspective(45.0, 1.0, 1.0, 100.0);
  matrix.lookAt(camera, 0, 0, 24, 0, 0, 0, 0, 1, 0);

// Create Vertex Object Buffers for the cubes models and
  // pre-processing for rendering.
  textx_gpu = new ModelArraysGPU(gl, models.textx, self.out);
  textx = new RenderColorPerVertex(gl, program, textx_gpu, self.out);

texty_gpu = new ModelArraysGPU(gl, models.texty, self.out);
  texty = new RenderColorPerVertex(gl, program, texty_gpu, self.out);

textz_gpu = new ModelArraysGPU(gl, models.textz, self.out);
  textz = new RenderColorPerVertex(gl, program, textz_gpu, self.out);

cubex_gpu = new ModelArraysGPU(gl, models.cubex, self.out);
  cubex = new RenderColorPerVertex(gl, program, cubex_gpu, self.out);

cubey_gpu = new ModelArraysGPU(gl, models.cubey, self.out);
  cubey = new RenderColorPerVertex(gl, program, cubey_gpu, self.out);

cubez_gpu = new ModelArraysGPU(gl, models.cubez, self.out);
  cubez = new RenderColorPerVertex(gl, program, cubez_gpu, self.out);

cube_center_gpu = new ModelArraysGPU(gl, models.cube_center, self.out);
  cube_center = new RenderColorPerVertex(gl, program, cube_center_gpu, self.out);

// - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
  // Setup of models to render the global axes
  x_axis_gpu = new ModelArraysGPU(gl, models.x_axis, self.out);
  y_axis_gpu = new ModelArraysGPU(gl, models.y_axis, self.out);
  z_axis_gpu = new ModelArraysGPU(gl, models.z_axis, self.out);

x_axis = new RenderColorPerVertex(gl, program, x_axis_gpu, self.out);
  y_axis = new RenderColorPerVertex(gl, program, y_axis_gpu, self.out);
  z_axis = new RenderColorPerVertex(gl, program, z_axis_gpu, self.out);

// Set the scaling for the global axes.
  matrix.scale(scale_axes, 0.4, 0.4, 0.4);

// Create a small sphere to render the path control points
  sphere_gpu = new ModelArraysGPU(gl, models.Sphere, self.out);
  sphere = new RenderColorPerVertex(gl, program, sphere_gpu, self.out);

// Set up callbacks for user and timer events
  self.events = new BezierEvents(id, self);
};

Use a parametric equation to calculate points along a path.
Intermediate points influence acceleration and deceleration.

Calculated Animation Properties:
speed : ---
acceleration : ---
frames per second : ---

Timing:
current frame 0 : 0 120
animation: start frame: end frame:

Control Points:
Scale <p1-p0> 0.10 : 0.0 1.0
---

Show: Process information Warnings Errors

Open this webgl program in a new tab or window

Conclusion

An animator can control the location, speed and acceleration of motion of an object over a path defined by using four control points, p0, p1, p2, and p3. Points p0 and p3 define the overall length of the path. The placement of the intermediate points, p1 and p2 control the speed and acceleration.

Glossary¶

speed: The change in an object’s location relative to changes in time.
acceleration: The change in speed over a time interval.
derivative: A mathematical operation that determines the “rate of change” in an equation.
Bezier parametric equation: A function of one variable, t, that calculates changes along a “path”.

Self Assessment¶

p0
Correct. p0 is the starting location.
p1
Incorrect.
p2
Incorrect.
p3
Correct. p3 is the ending location.

p0
Incorrect. p0 is the starting location.
p1
Correct.
p2
Correct.
p3
Incorrect. p3 is the ending location.

at p0 and p3.
Correct.
equally spaced along the path.
Incorrect. This produces constant speed, but does not start with a speed of zero.
equal to each other and at the path's midpoint.
Incorrect. The speed is not zero when the motion starts.
(1/4) the distance of the total motion.
Incorrect. The speed is not zero when the motion starts.

8.5 - Bezier Parametric Equations¶

Speed and Acceleration¶

Bezier Parametric Equations¶

Glossary¶

Self Assessment¶