8.3 - Basis Functions¶
A parametric equation allows us to calculate intermediate values between
two distinct values using a single parameter t. In the previous lesson
you studied an example for calculating points along a straight path between
two points, p1 and p2.
p = (1-t)*p1 + t*p2; // where t varies from 0.0 to 1.0
Mathematically this is a “weighted sum,” where each point on the path between
p1 and p2 is the sum of two percentages. This is a very simple
and elegant idea that can be extended in a variety of interesting ways.
Basis Functions¶
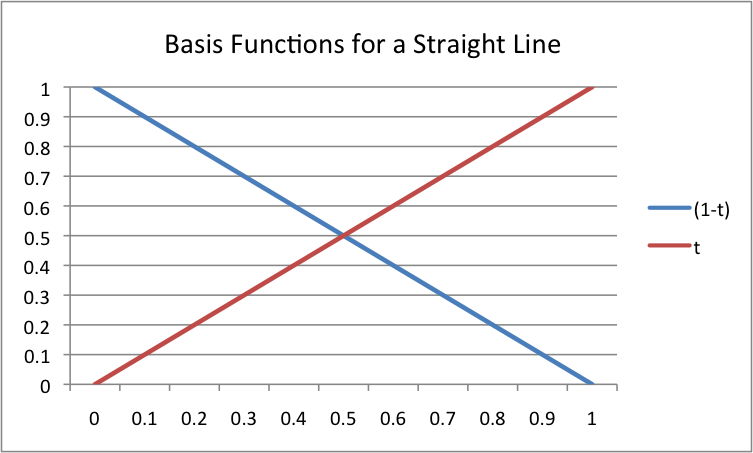
The functions that produce the fractions used for a parametric
equation are called basis functions . Let’s plot the basis functions
for the simple example above. The basis functions are (1-t) and (t).
A plot of these two functions for values of t between 0.0 and 1.0 gives
the straight lines in the diagram to the right. Please notice the following about these
basis functions:
- Every value for the basis functions is a fraction. They represent percentages.
- The basis functions sum to one for all values of
t. That is,(1-t) + t === 1.0. If this property is true for a set of basis functions, then all of the intermediate points on a path lie inside the convex hull of the points that define the path.
Here is the “big idea”:
Parametric Equations
Given discrete values at key frames, intermediate values can be calculated using a weighted sum of the discrete values. Basis functions calculate the appropriate weighting factors.
Glossary¶
- basis functions
- A set of functions that calculate the percentage of contribution a discrete value contributes to an intermediate value.
Self Assessment¶
- (t)
- Correct.
- (1-t)
- Correct.
- p1
- Incorrect. p1 is a constant that defines the starting value.
- p2
- Incorrect. p2 is a constant that defines the ending value.
Q-182: Given the parametric equation described in this lesson,
p = (1-t)*p1 + t*p2; // where t varies from 0.0 to 1.0
what are its basis functions? (Select all that apply.)