7.5 - Rotating a Camera (e.g., tilt) — Learn Computer Graphics using WebGL

Tilt Motion¶

To tilt a camera means you rotate a camera’s orientation around its u axis. You can tilt up (positive rotation) or tilt down (negative rotation).

As in the previous lesson, there are two basic ways to implement a tilt camera motion:

Modify the parameters of a call to the lookat function and then call lookat to create a camera transformation matrix, or
Directly modify the definition of a camera’s position and coordinate axes.

Let’s solve the problem both ways.

Use `lookAt` to Tilt¶

In the previous lesson you studied a class called LookAtCamera which defines a camera using two points and one vector: 1) the location of the camera, 2) the location of a point along it’s line-of-sight, and 3) a direction that is upwards. To “tilt” a camera, we add a new function to the LookAtCamera class called tilt.

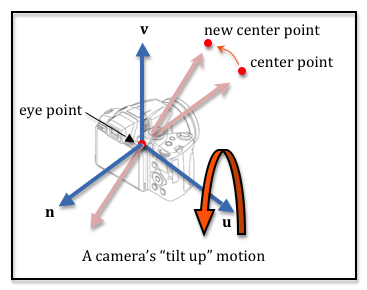
A tilt movement must change the center point. We need to rotate the location of the center point about the camera’s u axis, which will change the line-of-sight of the camera. Remember that the camera will be invalid if the line-of-sight and the up-vector are pointing in the same direction. Therefore, if the angle between the line-of-sight vector and the up-vector gets small, we need to rotate the up-vector to keep it away from the line-of-sight vector. The diagram illustrates a tilt movement.

The tilt function receives an angle, in degrees, which is the amount of rotation. If the angle is positive, the function will “tilt up”. If the angle is negative, the function will “tilt down”. The basic steps are:

Calculate the camera’s u axis.
Move the camera to the origin. This moves the eye point to the origin and it moves the center point to some location relative to the origin. You translate by (-eye_x, -eye_y, -eye_z). This is required because all rotation is about the origin.
Rotate the center point about the u axis by the angle of tilt.
Move the camera back to its original location. You translate the center point by (eye_x, eye_y, eye_z).
Use the lookAt function to recalculate the camera’s transformation matrix.

Note that all of the above operations need to be performed by 4-by-4 transformation matrices because you are not necessarily working in a plane that is parallel to the global axes.

Use the following demo to experiment with tilting a camera. Notice that tilting is always relative to the camera’s frame of reference. The code is editable if you want to experiment.

Show: Code Canvas Run Info

lookat_camera.js

/**
 * lookat_camera.js, By Wayne Brown, Spring 2016
 */

/**
 * The MIT License (MIT)
 *
 * Copyright (c) 2015 C. Wayne Brown
 *
 * Permission is hereby granted, free of charge, to any person obtaining a copy
 * of this software and associated documentation files (the "Software"), to deal
 * in the Software without restriction, including without limitation the rights
 * to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
 * copies of the Software, and to permit persons to whom the Software is
 * furnished to do so, subject to the following conditions:
 *
 * The above copyright notice and this permission notice shall be included in all
 * copies or substantial portions of the Software.

* THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
 * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
 * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
 * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
 * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
 * OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
 * SOFTWARE.
 */

"use strict";

/**------------------------------------------------------------------------
 * Store and manipulate a camera based on the parameters of the lookAt function.
 * @constructor
 */
window.LookAtCamera = function () {

// Constructor
  let self = this;

// Objects needed for internal elements and calculations
  let matrix = new GlMatrix4x4();
  let V = new GlVector3();
  let P4 = new GlPoint4();

// Camera definition at the default camera location and orientation
  self.eye       = P4.create(0, 0, 0, 1);  // (x,y,z,w), origin
  self.center    = P4.create(0, 0, -1, 1); // (x,y,z,w), down -Z axis
  self.up_vector = V.create(0, 1, 0);  // <dx,dy,dz>, up Y axis

// Create a matrix to hold the camera's matrix transform
  self.transform = matrix.create();

// Scratch objects for calculations
  let u, n, to_origin, rotate_matrix, move_back, temp_transform;
  u = V.create();  // u coordinate axis of camera
  n = V.create();  // n coordinate axis of camera
  to_origin = matrix.create();
  rotate_matrix = matrix.create();
  move_back = matrix.create();
  temp_transform = matrix.create();

/**----------------------------------------------------------------------
   * Using the current values for eye, center, and up, calculate a new
   * camera transformation matrix.
   */
  self.updateTransform = function () {
    // Calculate a new camera transform
    matrix.lookAt(self.transform,
                  self.eye[0], self.eye[1], self.eye[2],
                  self.center[0], self.center[1], self.center[2],
                  self.up_vector[0], self.up_vector[1], self.up_vector[2]);
  };

/**----------------------------------------------------------------------
   * Perform a truck operation on the camera
   * @param distance {number} How far to move the camera
   */
  self.truck = function (distance) {
    // Calculate the n camera axis
    V.subtract(n, self.eye, self.center);  // n = eye - center
    V.normalize(n);

// Calculate the u camera axis
    V.crossProduct(u, self.up_vector, n);
    V.normalize(u);

// Scale the u axis to the desired distance to move
    V.scale(u, u, distance);

// Add the direction vector to both the eye and center positions
    P.addVector(self.eye, self.eye, u);
    P.addVector(self.center, self.center, u);

self.updateTransform();
  };

/**----------------------------------------------------------------------
   * Perform a tilt operation on the camera
   * @param angle {number} How much to rotate the camera's orientation
   */
  self.tilt = function (angle) {
    // Calculate the n camera axis
    V.subtract(n, self.eye, self.center);  // n = eye - center
    V.normalize(n);

// Calculate the u camera axis
    V.crossProduct(u, self.up_vector, n);
    V.normalize(u);

// Move the center point so that the eye at the origin
    matrix.translate(to_origin, -self.eye[0], -self.eye[1], -self.eye[2]);
    matrix.rotate(rotate_matrix, angle, u[0], u[1], u[2]);
    matrix.translate(move_back, self.eye[0], self.eye[1], self.eye[2]);

// Calculate a transform for rotating the center point
    matrix.multiplySeries(temp_transform, move_back, rotate_matrix, to_origin);

// Rotate the center point
    matrix.multiplyP4(self.center, temp_transform, self.center);

// Rotate the up-vector about the u axis to make sure it does
    // not become co-linear with the n axis.
    matrix.multiplyV3(self.up_vector, rotate_matrix, self.up_vector);

self.updateTransform();
  };

self.updateTransform();
};

Perform a camera tilt motion.
The left canvas shows the relative location of the scene objects and the camera.
The right canvas shows the scene from the camera's vantage point.

Manipulate the lookAt function's parameters:
lookAt(M, eye_x, eye_y, eye_z, center_x, center_y, center_z, up_dx, up_dy, up_dz)

eye (0.0, 0.0, 5.0)	center (0.0, 0.0, 0.0)	up <0.0, 1.0, 0.0>
X: -5.0 +5.0	X: -5.0 +5.0	X: -1.0 +1.0
Y: -5.0 +5.0	Y: -5.0 +5.0	Y: -1.0 +1.0
Z: -5.0 +5.0	Z: -5.0 +5.0	Z: -1.0 +1.0

Show: Process information Warnings Errors

Open this webgl program in a new tab or window

You must study the above code carefully to understand camera movement. Please don’t skip the comment statements as you study the code.

Modify A Camera’s Definition¶

Let’s implement the “tilt” motion of a camera using the camera’s basic definition: a location and three coordinate axes. Using the AxesCamera class we introduced in the previous lesson, we can use the rotateAboutU function to implement a tilt motion because that is precisely what a tilt is. To tilt a camera we simply need to rotate the v and n coordinate axes about the u axis. The eye location of the camera does not change.

Please study the rotateAboutU function in the following demo program. This demo code is editable.

Show: Code Canvas Run Info

axes_camera.js

/**
 * axes_camera.js, By Wayne Brown, Fall 2017
 */

/**
 * The MIT License (MIT)
 *
 * Copyright (c) 2015 C. Wayne Brown
 *
 * Permission is hereby granted, free of charge, to any person obtaining a copy
 * of this software and associated documentation files (the "Software"), to deal
 * in the Software without restriction, including without limitation the rights
 * to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
 * copies of the Software, and to permit persons to whom the Software is
 * furnished to do so, subject to the following conditions:
 *
 * The above copyright notice and this permission notice shall be included in all
 * copies or substantial portions of the Software.

* THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
 * IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
 * FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
 * AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
 * LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
 * OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
 * SOFTWARE.
 */

"use strict";

/**------------------------------------------------------------------------
 * Store and manipulate a camera based on its location and its
 * local coordinate system.
 * @constructor
 */
window.AxesCamera = function () {

// Constructor
  let self = this;

// Objects needed for internal elements and calculations
  let matrix = new GlMatrix4x4();
  let V = new GlVector3();
  let P = new GlPoint4();

// Camera definition at the default camera location and orientation.
  self.eye = P.create(0, 0, 0, 1);  // (x,y,z,w), origin
  self.u   = V.create(1, 0, 0);  // <dx,dy,dz>, +X axis
  self.v   = V.create(0, 1, 0);  // <dx,dy,dz>, +Y axis
  self.n   = V.create(0, 0, 1);  // <dx,dy,dz>, +Z axis

// Create a matrix to hold the camera's matrix transform
  self.transform = matrix.create();

// Scratch objects for calculations
  let u_scaled;
  u_scaled = V.create();  // a scaled u coordinate axis of camera
  let temp_transform;
  temp_transform = matrix.create();

/**----------------------------------------------------------------------
   * Using the current values for eye, u, v, and n, set a new camera
   * transformation matrix.
   */
  self.updateTransform = function () {
    let tx = -V.dotProduct(self.u, self.eye);
    let ty = -V.dotProduct(self.v, self.eye);
    let tz = -V.dotProduct(self.n, self.eye);

// Use an alias for self.transform to simplify the assignment statements
    let M = self.transform;

// Set the camera matrix
    M[0] = self.u[0];  M[4] = self.u[1];  M[8]  = self.u[2];  M[12] = tx;
    M[1] = self.v[0];  M[5] = self.v[1];  M[9]  = self.v[2];  M[13] = ty;
    M[2] = self.n[0];  M[6] = self.n[1];  M[10] = self.n[2];  M[14] = tz;
    M[3] = 0;          M[7] = 0;          M[11] = 0;          M[15] = 1;
  };

/**----------------------------------------------------------------------
   * Perform a "truck" operation on the camera
   * @param distance {number} the distance to move the camera
   */
  self.truck = function (distance) {
    // Scale the u axis to the desired distance to move
    V.scale(u_scaled, self.u, distance);

// Add the direction vector to the eye position.
    P.addVector(self.eye, self.eye, u_scaled);

// Set the camera transformation. Since the only change is in location,
    // change only the values in the 4th column.
    self.transform[12] = -V.dotProduct(self.u, self.eye);
    self.transform[13] = -V.dotProduct(self.v, self.eye);
    self.transform[14] = -V.dotProduct(self.n, self.eye);
  };

/**----------------------------------------------------------------------
   * Rotate the orientation of the camera about the u axis.
   * @param angle {number} the angle of rotation
   */
  self.rotateAboutU = function (angle) {
    // Create a rotation matrix with the u axis as the pivot.
    matrix.rotate(temp_transform, angle, self.u[0], self.u[1], self.u[2]);

// Perform the rotation
    matrix.multiplyV3(self.v, temp_transform, self.v);
    matrix.multiplyV3(self.n, temp_transform, self.n);

self.updateTransform();
  };

/**----------------------------------------------------------------------
   * Rotate the orientation of the camera about the v axis.
   * @param angle {number} the angle of rotation
   */
  self.rotateAboutV = function (angle) {
    // Create a rotation matrix with the v axis as the pivot.
    matrix.rotate(temp_transform, angle, self.v[0], self.v[1], self.v[2]);

// Perform the rotation
    matrix.multiplyV3(self.u, temp_transform, self.u);
    matrix.multiplyV3(self.n, temp_transform, self.n);

self.updateTransform();
  };

/**----------------------------------------------------------------------
   * Rotate the orientation of the camera about the n axis.
   * @param angle {number} the angle of rotation
   */
  self.rotateAboutN = function (angle) {
    // Create a rotation matrix with the n axis as the pivot.
    matrix.rotate(temp_transform, angle, self.n[0], self.n[1], self.n[2]);

// Perform the rotation
    matrix.multiplyV3(self.u, temp_transform, self.u);
    matrix.multiplyV3(self.v, temp_transform, self.v);

self.updateTransform();
  };

self.updateTransform();
};

Perform a camera tilt motion.
The left canvas shows the relative location of the scene objects and the camera.
The right canvas shows the scene from the camera's vantage point.

Manipulate the camera's definition:

eye (0.0, 0.0, 5.0)	u <1.00, 0.00, 0.00> v <0.00, 1.00, 0.00> n <0.00, 0.00, 1.00>
X: -5.0 +5.0	u angle: -180.0 +180.0
Y: -5.0 +5.0	v angle: -180.0 +180.0
Z: -5.0 +5.0	n angle: -180.0 +180.0

Show: Process information Warnings Errors

Open this webgl program in a new tab or window

Summary¶

A camera movement that involves rotation will rotate about one of the current axes of the camera’s coordinate system. If a camera tilts, the rotation is about the u axis. If a camera pans, the rotation is about the v axis. If a camera cants, the rotation is about the n axis. Camera motion is almost always relative to a camera’s current frame of reference.

As in the previous lesson, manipulating the actual camera definition (a point and 3 axes) requires less computation but more mathematical understanding of the camera matrix transform.

Glossary¶

tilt camera: Rotate a camera upwards or downwards, keeping its location unchanged.
pan camera: Rotate a camera left or right, keeping its location unchanged.
cant camera: Rotate a camera about its line-of-sight, keeping its location unchanged.

Self Assessment¶

tilt

lookAt

center point
Correct. Changing the center point moves the camera's line-of-sight but leaves the position of the camera unchanged.
eye and up vector
Incorrect. The up-vector does not control the camera's exact orientation.
center point and up vector
Incorrect. The up-vector does not control the camera's exact orientation, but the center point does.
up vector only
Incorrect. The up-vector does not control the camera's exact orientation.

tilt

u axis
Correct. You are rotating "up" or "down" from the camera's current orientation.
v axis
Incorrect. Rotating about the v axis would be a pan motion.
n axis
Incorrect. Rotating along the n axis would be a cant motion.

tilt

sine

cosine

sine and cosine are only defined in a plane, but a tilt is relative to a camera's current orientation.
Correct. The tilt rotation is about an arbitrary axis, not the x, y or z axis.
well, actually you could use normal trig calculations.
Incorrect. Actually, you can't!
sine and cosine only work in the x-y plane.
Incorrect. Sine and cosine only work in a plane, but are not restricted to the x-y plane.
matrix transforms minimize the calculations required.
Incorrect. Matrix multiplies are computationally expensive.

7.5 - Rotating a Camera (e.g., tilt)¶

Tilt Motion¶

Use lookAt to Tilt¶

Modify A Camera’s Definition¶

Summary¶

Glossary¶

Self Assessment¶

Use `lookAt` to Tilt¶