Mapping Values in a Range¶

Linear Mapping¶

Given a range of values between A and B, we want to map them into a different range of values between C and D. In addition, we want the relative distance between any two points in each range to remain constant. Or, said another way, we want points to be equally distributed in both ranges. The image below illustrates the two ranges. A mapping that maintains a constant ratio between points is a linear mapping.

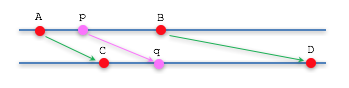
A linear mapping requires two operations: a scaling operation to make the ranges the same size, and an offset operation to make the ranges align. You can think about solving this problem in various ways. Let’s walk through three different solutions and show that in each case you get the same answer. To make the discussion clear, let’s exactly define our problem.

Given a value p in the range A to B, calculate a point q in the range C to D that is in the same relative location.

• Solution 1:
  • Since scaling is always relative to the origin, and we need to scale the range from A to B to make it the same size as the range C to D, let’s shift the range A to B to the origin. We can do this by subtracting A from p. p-A
  • Scale p by the ratio of the range sizes, (D-C)/(B-A). (p-A)*(D-C)/(B-A)
  • Now shift this value to the start of the “C to D” range by adding C. Therefore, our equation is q = (p-A)*(D-C)/(B-A) + C
    
    
• Solution 2:
  • Because the relationship between the points p and q must maintain relative distances, the ratio of their distances must be equal to the ratio of the range sizes. Therefore, (p-A)/(q-C) = (B-A)/(D-C)
  • Solving this equation for q, results in q = (p-A)*(D-C)/(B-A) + C
    
    
• Solution 3:
  • Using a parametric equation for the range from A to B, there is a value for t that calculates p. That is, p = (1-t)*A + t*B. Solving for t gives t=(p-A)/(B-A).
  • Since t is a percentage of the distance between A and B, this percentage must be the same for the location of q between C and B. Therefore, we use this value for t in a parametric equation for the range between C and D. The equation q = (1-t)*C + t*D becomes q = (1-(p-A)/(B-A))*C + (p-A)/(B-A)*D. Simplifying this equation gives q = (p-A)*(D-C)/(B-A) + C.
    
    

If you rearrange the terms in the solution for q, you end up with a scale factor and an offset. Specially,

scale = (D-C)/(B-A)
offset = -A*(D-C)/(B-A) + C    or offset = -A*scale + C
q = p*scale + offset

Let’s work a specific example. We want to take the values between 12 and 22 and map them into a range from 6 to 7. The ratio between these two ranges is (7-6)/(22-12) = 1/10. The offset is -12*(1/10) + 6 = 4.8. The linear mapping formula becomes q = p*(1/10) + 4.8. If the formula is applied to all of the whole numbers in the range 12 to 22, you get equally spaced values in the range 6 to 7, as shown below.

Glossary¶

mapping

a function that converts a set of inputs into an output value.

linear mapping

a function that converts a location in one range of values into a proportionally equivalent location in a different range.