3.7 - Modeling Surfaces¶

Flat Surfaces?¶

One Normal Per Face¶

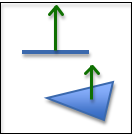
One normal per face.

In the lesson on modeling volumes we discussed “normal vectors,” which point in the direction that is 90 degrees to every point on the front face of a triangle. If we model a surface using a single normal vector, we assume that the triangle is perfectly flat. This is referred as “flat shading” because every pixel on the face will have the same color.

If a normal vector for a triangle is not specified, it can be calculated by taking the cross-product of two of the triangle’s edges, assuming the correct winding order for the vertices.

One Normal Vector Per Vertex¶

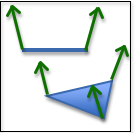
One normal per vertex

If you specify a different normal vector for each vertex of a triangle, you can calculate a different color for each vertex. Then the colors for each pixel across the face can be interpolated from the colors at the vertices. If the vertex normal vectors are set appropriately, the face can appear curved (instead of flat). (This technique is named after its inventor and is called Gouraud shading)

You will get more accurate coloring across a face if you interpolate the normal vectors at the vertices across the face and then recalculate the fragment color using the interpolated normal vector. This method requires more computation, but gives smoother color gradients. This is called Phong shading.

Both techniques are referred to as “smooth shading”.

Flat vs. Smooth Shading. (1)

One Normal Vector Per Pixel¶

One normal per pixel

You can control the color of individual pixels on the surface of a triangle by specifying a unique normal vector for each pixel. This is done by creating an image, where each “pixel” in the image is not treated as a RGB value, but rather as a <dx,dy,dz> normal vector. This is called a bump map. Here is an example rendering using bump maps.

A “bump mapped” object. (2)

As we store more and more data about the properties of a surface we can get greater and greater realistic results.

Many of the techniques used to model surface properties have the word “map” in them, such as “bump map”, so let’s backtrack and discuss the general concept of a “mapping.”

What is a Mapping?¶

In mathematics, a mapping is a function that converts a set of inputs into an output value. There are two basic ways this can be done:

• Perform calculations on the inputs to produce the output value. This is called “procedural mapping.”
• Lookup the output value from a list of possible values. This is called a “table lookup.”

For computer graphics, the input to a mapping is typically a location on a surface, and the output is a color, a normal vector, or any other property that is changing across the surface of a triangle. Let’s take a look at a specific example called texture mapping which takes a location on a surface and outputs a specific color for that location.

Procedural Texture Mapping¶

A procedural texture map is a function that converts input values into a color using a calculation. The results of the calculation can be used to select a color, or the calculated values can be used to create a color. There is no limit to the number of possible patterns that can be calculated. The following example function produces a black and white checkerboard pattern that is 10 pixels wide.

function checkerboard(x,y) {
  if ( floor(x/10) + floor(y/10) mod 2 == 1) {
    color = [0, 0, 0, 1]; // black
  } else {
    color = [1, 1, 1, 1]; // white
  }
  return color;
}

The input values can be anything you want to base the coloring on. A 1D texture map takes a single input value and returns a color. A 2D texture map takes two input values and returns a color. A 3D texture map takes three input values and returns a color.

Image Texture Mapping¶

“Table lookup” texture mapping is typically done using an image. An image is a 2D array of color values. Given a row and column value, it is trivial to return the color of the pixel at a particular location in the image. In pseudo code, such a texture map would look like this:

function getColor(image, x, y) {
  return image[x][y]; // the color of the indicated pixel
}

Images are a convenient way to specify a set of color values for the face of a triangle. However, images are always rectangles and WebGL only renders triangles. We need a way to specify which pixels inside an image contain the colors for a triangle’s face.

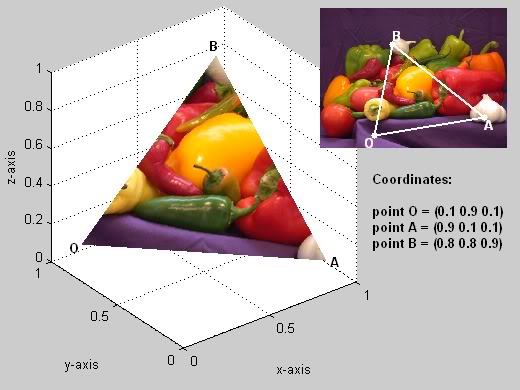
An image being used as a texture map. (3)

“Texture coordinates” specify which location in an image corresponds to a triangle’s vertices. To make texture coordinates work for any image, the locations are specified in percentages. For example, 0.0 is the left edge of an image, 1.0 is the right edge, and 0.5 is the middle. The image to the left shows an example. Vertex B is mapped to a specific location in the image with texture coordinates (0.31, 0.74) because the color in the image we want to be displayed at vertex B is 31% from the left edge and 74% from the bottom edge. Once the three, 3D vertices are mapped to corresponding locations in the image, the interior locations can easily be calculated.

Note that if the proportions of a 3D triangle are not proportional to the area on the image, the ‘picture’ displayed on the 3D triangle will be distorted. Assigning texture coordinates that do not distort an image is difficult to do manually. Tools like Blender greatly assist in creating appropriate texture coordinates.

Surface Properties¶

In addition to texture mapping, many other techniques have been developed to model the surface properties of an object. Here are few:

• bump maps - maps a location on a triangle to a variation in the surface normal. The variation values are typically stored in an “image” where each “pixel” value is an offset to the primary surface normal vector.
  
  
• normal maps - maps a location on a triangle to a surface normal. The surface normals are often stored in an “image” where each “pixel” is not a RGB value, but rather a <dx, dy, dz> vector.
  
  
• displacement maps - maps a location on a triangle to a variation in surface height. The height values can be stored in a “monochrome image” where each “pixel” value is interpreted as a height value instead of a color value.
  
  

These techniques are all called “maps” because they associate a location on a triangle with some property of the surface at that location. Again note that these techniques can be “procedural” (which calculates the property), or use a “table lookup” (which pulls the property from a predefined array of values).

WebGL Implementation¶

The techniques we have discussed will be implemented in WebGL shader programs that execute the graphics pipeline. One normal vector per face and one normal vector per vertex are implemented in vertex shaders. Phong shading, texture mapping, and other “mapping” techniques are implemented in fragment shaders because they calculate the color of individual pixels. Image based texture mapping is performed by:

• Downloading an appropriate image from the server.
• Creating a GPU texture object and saving the image to the GPU’s memory.
• Using a table lookup function in your fragment shader to get a color out of the image for a specific pixel.

Exact implementation details for texture mapping will be given in Chapter 10.

Summary¶

Very realistic renderings can be produced by using these surface property modeling techniques. To produce life-like renderings it is common to use some combination of many or all of these techniques.

Surface properties are only part of the modeling we need to produce realistic images. How the surface reflects light is the other critical part. The next lesson explains how to model light sources.

Glossary¶

material properties

A mathematical description of a “material” that forms the surface of a triangle.

flat shading

A single color is calculated for the face of a triangle.

Gouraud shading

A different color is calculated for each vertex of a triangle. The color of interior pixels are interpolated from the colors at its vertices.

Phong shading

Interpolate normal vectors across the face of a triangle and use these normal vectors to calculate a unique color for each pixel.

smooth shading

Use either Gouraud shading or Phong shading to vary the colors over a triangle’s face.

mapping

A function that converts a set of inputs into an output value.

bump map

Use a unique normal vector at each pixel to calculate a color. The normal vectors are designed to give the impression of bumps on the surface.

texture map

Map a location on the surface of a triangle to a color.

procedural texture map

A texture map implemented by calculations in GLSL code.

image texture map

A texture map implemented using an image and “table lookups” using texture coordinates.

texture coordinates

A location in a table of color values. The location is a percentage of the table’s size.

Self Assessment¶